

MATEMATICAS |
Caos transitorio en mapas unidimensionales con tres puntos fijos |
RESUMEN [ABSTRACT]
Dentro de los estudios de dinámica no lineal y caos se ha detectado el llamado caos transitorio, donde el comportamiento irregular y aperiódico tiene inicialmente la "apariencia" de caos pero después de cierto tiempo la solución termina por estabilizarse o se dirige a un comportamiento donde podemos predecir el futuro. Se han encontrado distintos ejemplos de caos transitorio y en este trabajo mostramos un nuevo caso. Aparte del caos generado por ecuaciones diferenciales no lineales donde el tiempo es continuo existe el caos producido en fórmulas recursivas (incluso las hay muy simples) donde el tiempo se lo toma discreto, son las llamadas ecuaciones de diferencias o mapas. Este estudio muestra caos transitorio en un tipo de estos mapas: unidimensionales con tres puntos fijos.
Introducción
La dinámica comienza con Newton como ciencia que estudia el movimiento, es decir, se interesa por la posición y velocidad de un cuerpo en función del tiempo. Estas magnitudes están relacionadas por medio de la ley de Newton, que establece que la fuerza total que actúa sobre un cuerpo (idealizado como partícula infinitesimalmente pequeña) es proporcional a la aceleración de dicho cuerpo, con la masa del cuerpo como la constante de proporcionalidad. En términos matemáticos la ley de Newton es una ecuación diferencial. Resolviéndola, cuando es posible, obtenemos la posición (cuya derivada segunda es la aceleración) y la velocidad (cuya derivada es la aceleración) del cuerpo en cuestión. Este es uno de los ejemplos mas sencillos de lo que se llama sistemas dinámicos, es decir sistemas donde una o mas magnitudes que dependen del tiempo están regidos por un sistema de una o más ecuaciones diferenciales. En ejemplos distintos y más generales de sistemas dinámicos las variables pueden ser el número de insectos de un determinado tipo, la aparición aperiódica de las epidemias, las oscilaciones registradas de un terremoto, la actividad del corazón graficada por un electrocardiograma, o el índice del mercado de acciones. Siempre estudiando estas variables en función del tiempo, que están determinadas por las ecuaciones que las gobiernan. Es decir, se trata de sistemas deterministas que dependen de las condiciones iniciales. Sin emabrgo, en algunos casos el comportamiento es tan irregular, que tendremos caos. El caos, que puede darse en los ejemplos dinámicos citados, fue vislumbrado por Poincaré a fin del siglo XIX, y puesto de manifiesto por el meteorólogo E. Lorenz (1963): El pronóstico meteorológico es un importante servicio que nos llega a través del periódico, la radio, la televisión e internet. Pero nos suelen pronosticar solamente los 4 días venideros. Y a veces es incorrecto! Sería interesante, para una pareja de novios, poder conocer el clima del día del casamiento con meses de anticipación. O para una universidad que planee la graduación y fiesta al aire libre. Esta mejora en el pronóstico estaba buscando Lorenz tratando de hacer un modelo físico-matemático del clima. Tenía 12 ecuaciones que logró simplificar a 3. Pero la solución que arrojó su computadora Royal McBee mostraba un comportamiento irregular y aperiódico. Es más, cambiando una milésima sus condiciones iniciales, para un determinado día, obtenía un comportamiento muy distinto del pronóstico futuro próximo. Las ecuaciones diferenciales de Lorenz son no lineales. En las ecuaciones no lineales, a diferencia de lo que ocurre cuando las ecuaciones son lineales, la suma de dos soluciones no necesariamente es solución, o dicho de otra manera, el resultado de un determinado proceso no puede obtenerse estudiando 2 procesos distintos más sencillos, para luego sumar sus resultados. En estos sistemas no lineales deterministas diremos que hay caos cuando la solución varía en forma irregular y aperiódica siendo imposible prever el comportamiento a grandes tiempos y donde hay una gran sensibilidad a las condiciones iniciales.
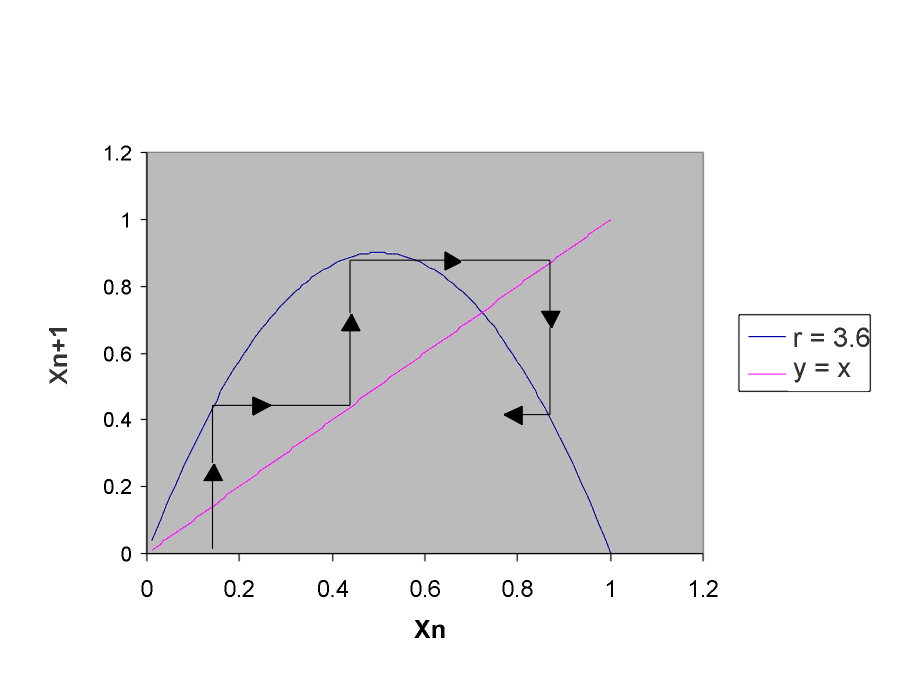
Figura 1: Mapa logístico
En cuanto a la sensibilidad a las condiciones iniciales se lo ha ejemplificado con el llamado "efecto mariposa": de dos mariposas que aletean en Hong Kong, una no produce nada especial y la otra provoca un huracán en el Caribe.
También hablamos de sistemas dinámicos cuando la o las variables dependen de un tiempo discreto. Es decir, en vez de hacer correr los segundos y los minutos continuamente, decimos por ejemplo: en el año 1995 se produjeron 68 casos de paludismo en tal zona, en el año 1996 hubo 124 casos, en 1997 ..., o sea saltamos discretamente de año en año. Es el caso de las fórmulas de recurrencia o mapas con los cuales trabajaremos en este artículo, que son de gran interés porque nos dan ejemplos sencillos de caos. Incluso pueden generarse usando el programa Excel.
La primera aplicación comercial de la teoría del caos la realizó la compañía Goldstar en 1993. Consistió en diseñar un lavarropas que en vez de girar en forma continua o de alternar el giro en forma periódica, giraba caóticamente. Al "mezclarla" más de esta manera, la ropa resultó mejor lavada.
Mapas, Caos y Caos Transitorio
El mapa unidimensional más conocido es el mapa logístico (May, 1976; Strogatz, 1994):
xn+1 = r (xn — xn2)
Se trabaja en el cuadrado unidad. Partimos de la condición inicial x0, con la fórmula sacamos el x1 que pasa a ser usado como el x0 del nuevo cálculo, y así sucesivamente. Esta recurrencia se visualiza bien usando la "telaraña" de la Figura 1: dado el x0 en las abscisas "subo" a la función cuadrática y obtengo x1 de allí me desplazo horizontalmente hasta la recta a 45º, vuelvo a subir y obtengo x2 y así sucesivamente. Llamamos puntos fijos a las intersecciones de la cuadrática con la recta a 45º. Punto fijo es aquel que una vez alcanzado se repite indefinidamente al usar la fórmula de recurrencia. Punto fijo estable será cuando los valores próximos, mediante la fórmula, tienden a él y punto fijo inestable cuando los valores próximos tienden a alejarse de él.
El comportamiento de la solución a tiempos largos (la telaraña ha dado gran cantidad de vueltas), lo que aquí sería n grande, va a depender del valor de r. Los valores más interesantes de r están en el intervalo [0, 4]. Para r < 1, xn tiende a cero. Para 1 < r < 3, la solución se estabiliza tendiendo al punto fijo. Desde r = 3 se produce la "bifurcación". Es decir, que la solución tiende a grandes n a dos valores que se van alternando. A esto se lo llama período 2. En r = 3.44 ... se produce otra bifurcación, nace el período 4 y así sucesivamente hasta r = 3.56 ... donde nace el caos (Figura 2).
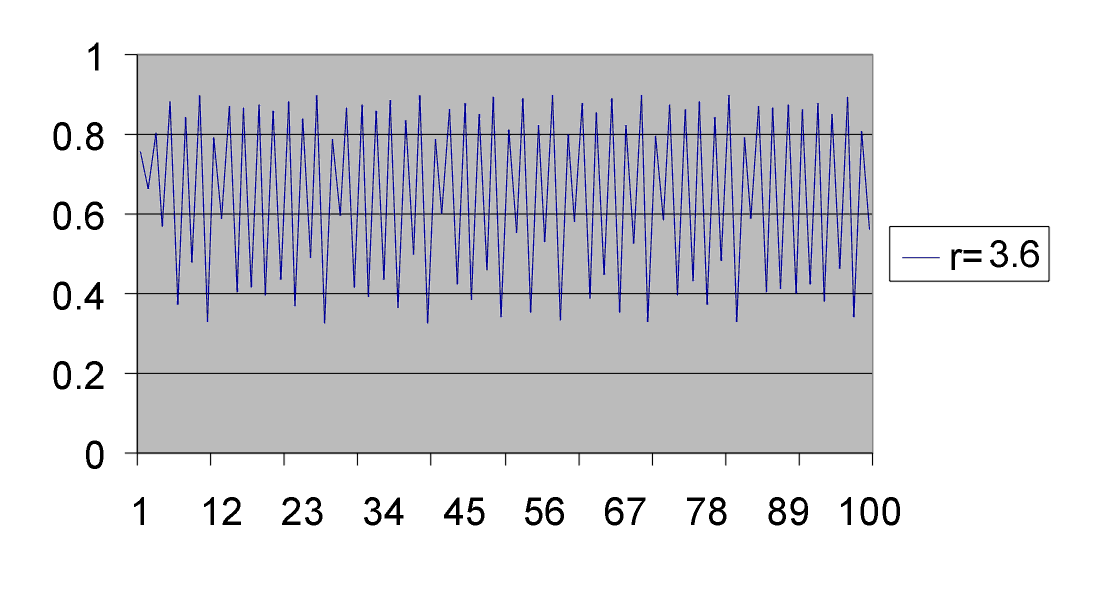
Figura 2: Caos en mapa logístico
Desde este valor de r hasta r = 4 tenemos caos, excepto para algunas "ventanas" (Strogatz, 1994). Decimos que el mapa logístico posee una ruta al caos por bifurcaciones. Para un estudio profundo del mapa logístico ver Strogatz, 1994.
El caos transitorio ha sido extensivamente estudiado para el mapa logístico (Woltering & Markus, 2000). Estos autores tomaron r = 4 + d , donde d es un número muy chico ( d « 1 ). Cuando la órbita explora el entorno del máximo, se sale del cuadrado unidad y diverge. Pero por ser d tan pequeño, la órbita "tarda" un tiempo en explorar los puntos superiores para luego tender a - ![]() : tenemos caos transitorio porque aparecen números sin ningún tipo de orden lo que "aparenta" ser caos, pero luego empiezan a salir números negativos que tienden al infinito negativo. Como sabemos con seguridad que va al infinito ya no hay caos y por eso se llama a esa sucesión de números "caos transitorio".
: tenemos caos transitorio porque aparecen números sin ningún tipo de orden lo que "aparenta" ser caos, pero luego empiezan a salir números negativos que tienden al infinito negativo. Como sabemos con seguridad que va al infinito ya no hay caos y por eso se llama a esa sucesión de números "caos transitorio".
Nosotros estudiamos el mapa unidimensional simétrico, siempre dentro del cuadrado unidad:
xn+1 = r (1 - cos2(p xn)) (1)
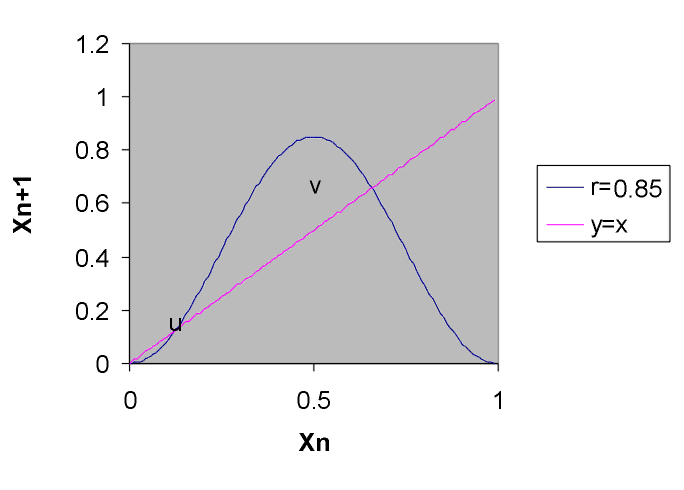
Figura 3: Mapa unidimensional con 3 puntos fijos
Encontramos tres puntos fijos como muestra la figura 3 y los llamamos: 0, u y v. El cero es un punto fijo estable para la cuenca de condiciones iniciales [0, u) U (1 - u, 1]. El punto fijo u depende de r y es siempre inestable. El punto fijo v también depende de r y pasará de ser estable a inestable cuando (Strogatz, 1994):
|f’(v) = 1| (2)
A partir de este punto tenemos la primera bifurcación y corresponde al valor r = 0.62... y, análogamente al mapa logístico, aumentando el r se obtiene una ruta al caos por bifurcaciones. A partir de r = 0.74 ... tenemos caos. En este caso el caos solo se da para las condiciones iniciales comprendidas en (u, 1 - u).
Sin embargo, se llega a un valor de r para el cual:
f(r) = u = 1 — r (3)
Ver figura 4.
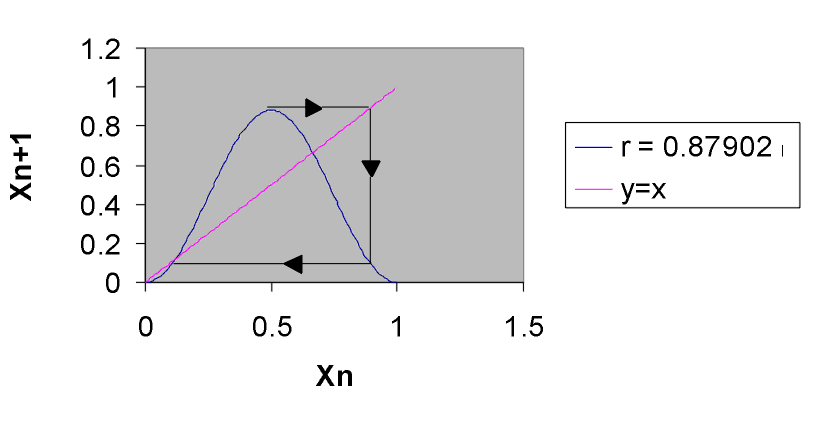
Figura 4: Telaraña del caos transitorio
r = 0.879019
u = 0.120981 (4)
f(r) = 0.1209814
En este caso tenemos caos real (Figura 5 con n = 2000)

Figura 5: Caos real en Ec. (1)
En cambio para:
r = 0.879021
u = 0.12098 (5)
f(r) = 0.120978
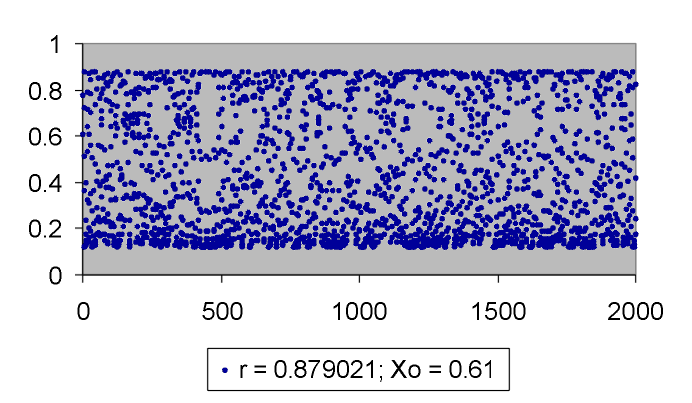
Figura 6: Caos transitorio no detectado hasta n = 2000
Las órbitas que exploran puntos cercanos al máximo r caen en la cuenca del 0, es decir en el intervalo [0, u) U (1 - u, 1] pero al haber pocos puntos que caigan en esta cuenca, la órbita puede ser larga y su aspecto es el del caos, aunque sabemos que se trata de caos transitorio. Dependiendo de la condición inicial el periódo transitorio será más o menos largo. La figura 6 muestra caos transitorio no detectado para r = 0.879021 y condición inicial x0 = 0.61, hasta n = 2000 tenemos caos aparente. En la figura 7 para el mismo valor de r pero con x0 = 0.62 la órbita cae a cero aproximadamente en 1075: Tenemos caos transitorio. Dependiendo de x0 la órbita tarda más o menos en caer a cero.
El exponente de Liapunov es un valor que indica la presencia de caos (Strogatz, 1994). Si éste es positivo indica que para pequeñas diferencias de condiciones iniciales las órbitas se separan exponencialmente (caos real). Un exponente de Liapunov negativo significa que estamos en el caso de un punto fijo estable o de un ciclo. Si el exponente de Liapunov es - ![]() , tenemos un punto fijo o un ciclo superestable. El cálculo de este exponente envuelve una suma (ver la expresión matemática del exponente de Liapunov en Strogatz, 1994) sobre los
, tenemos un punto fijo o un ciclo superestable. El cálculo de este exponente envuelve una suma (ver la expresión matemática del exponente de Liapunov en Strogatz, 1994) sobre los ![]() términos de la órbita. En la práctica se lo aproxima sumando un número grande de términos. Por eso el caos transitorio estudiado podrá dar equivocadamente positivo si no tomamos una cantidad suficientemente grande de puntos (zona del caos aparente antes de ir a cero, figura 7). Aplicando correctamente la fórmula para nuestro caso de caos transitorio se obtiene un exponente de Liapunov -
términos de la órbita. En la práctica se lo aproxima sumando un número grande de términos. Por eso el caos transitorio estudiado podrá dar equivocadamente positivo si no tomamos una cantidad suficientemente grande de puntos (zona del caos aparente antes de ir a cero, figura 7). Aplicando correctamente la fórmula para nuestro caso de caos transitorio se obtiene un exponente de Liapunov -![]() , indicando que el cero, adonde tienden los valores (figura 7), es un punto fijo superestable.
, indicando que el cero, adonde tienden los valores (figura 7), es un punto fijo superestable.
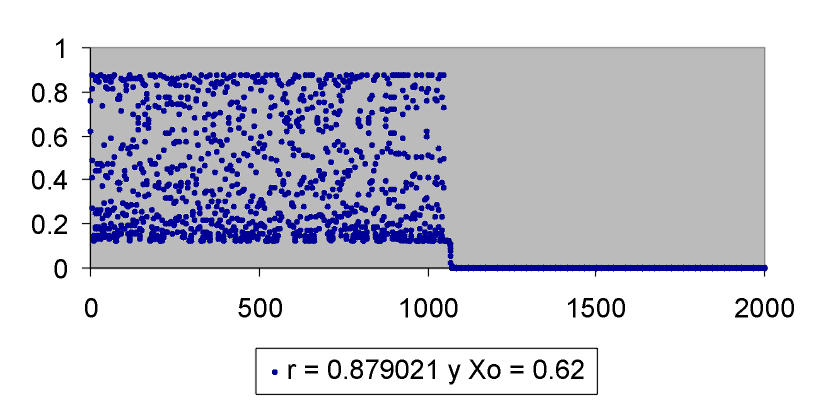
Figura 7: Caos transitorio
Unos resultados análogos se obtienen con el mapa asimétrico:
xn+1 = r (cos(p xn/2) - cos2(p xn/2)) (6)
Conclusión
Hemos visto un nuevo tipo de caos transitorio, el que aparece en mapas unidimensionales con tres puntos fijos. Estos estudios de mapas son sólo una simplificación matemática de los sistemas físicos y biológicos. La previsión y control del caos es algo altamente interesante en temas como los terremotos o la fibrilación del corazón. Podemos concluir que al igual que en otros casos de caos transitorio anteriormente descubiertos, el tiempo de caos aparente hasta la estabilización puede ser arbitrariamente largo, y por tanto es importante conocer si se trata de caos transitorio o caos real.
Referencias Bibliográficas
•Lorenz, E. N. (1963). Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130
•May, R. M. (1976). Simple Mathematical models with very complicate dynamics. Nature 261, 459
•Strogatz, S. H. (1994). Nonlinear dynamics and chaos. Perseus Books, Reading, Massachusetts
•Woltering M. and Markus M. (2000) Riddled-like basins of transient chaos. Phys. Rev. Lett. 84, 630
Puntos de interés
http://www.duke.edu/~mjd/chaos/chaos.html
http://library.thinkquest.org/3120/
http://members.home.net/jason.yiin/chaos.htm
http://math.gmu.edu/~tsauer/chaos/intro.html